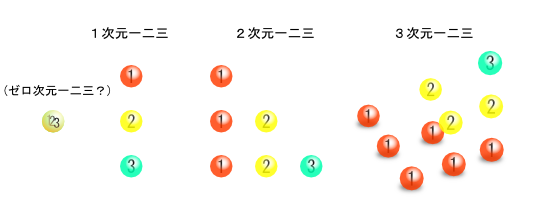
「何回宣伝するんだ」って感じですが、またまた貼っちゃうこの画像
日月神示の、いわゆる「一二三」が「3」になったり「10」になったりする
仮説?(妄想?)ですが、これを並んだ数列として表せば
「こうなるのでは?」が今回の記事です。最初に予防線を張りますが、
数学的にはたぶん間違ってる事をヌケヌケと書きます。
向こうのブログでは「一二三」までの数字、
「1・3・6・10・15・・・55」の行まででしたが、
こちらは「・・・八九十」まで、さらに行を2列追加します。
この五行だけでも規則性が見えてくると思います。
左下から右上に走る「◯・1・2・6・20・70」のラインを軸に、
左右対称ならぬ縦横が対称になっています。
さらに行と行の間に成り立つ「比率」の法則も見つけることが出来ます。
「2/2 3/2 4/2 5/2」という分数がその比率です。
どういう理屈でこんなキレイな階段状の比率になるのか、
数学に詳しい人ならスラスラっと説明してくださるのでしょうか。
見つけた僕は「ずいぶんうまい具合に成り立ってるなあ」と驚きましたが、
余計なことにも気づいてしまいました。
「一番左にある◯◯◯◯◯も、この法則に従って比率を出せそうだな?」
まさに机上の空論ですが「0/1?」「1/2?」「2/3?」「3/4?」という
「?」のついてるのがその比率たちです。
なんにも存在しない「◯(ゼロ)」に比率があるなんてオカシナ話ですが、
オカシナ自分はさらに妄想を膨らませていました。
「これは五段に重なった、たとえば〈1・1・1・1・1〉が同じ数字
(比率)だと成り立つ計算だけど、何にもない◯・◯・◯・◯・◯の方を
同一だと見なしたらどうなるんだろうか?」
一番下の「0/1」はどうしようもないというか、無い袖は振れないというか
比率を合わせられないので、「2:1」「3:2」「4:3」の比率だった
4つの「◯」を全て同じ「1:1:1:1」にしたのが↓下図↓です。
こうすれば4つの◯は比率的に同一「12:12:12:12」
(=「1:1:1:1」)になります。
せっかくの一桁が「12分のいくら」というムダにデカい数字になって、
階段状の比率も消えてしまいましたが、同じ行の分子分母が何倍かに
なっただけで、その階段状の比率は維持されています。
分数をわかりやすくするとこんな感じ
その結果「1」「1」「1」「1」という同一のものから
「12:24」=「1:2」
「12:18」=「2:3」
「12:16」=「3:4」という比率が生まれてしまいました。
「ナニ言ってんの?」と困惑されそうなのは判りますが、
勢いで押し切ります!最初に紹介した仮説?(妄想?)では
「この変換を次元と関係してるのでは?」と推察していました。
こんな風に↓
つまり一番下の「1・1・1・・・1」は一次元 「1から10」は二次元、
「1から55」は三次 「1から220」は4次元というように、
上に行くに従って次元が上がって
一番上の「1・5・15・・・715」は五次元になるのでは?
と同じ仮説の仮説を立ててみました。
今回の数列だと
二次元の「1」と三次元の「1」は「12:24」=「1:2」?
三次元の「1」と四次元の「1」は「12:18」=「2:3」?
四次元の「1」と五次元の「1」は「12:16」=「3:4」?
どう考えても「1」と「1」は同じものだと思いますが、
「1」より前にある「◯」を基準にして、
さらに階段状に並ぶ比率を使って逆算すれば、
次元の違う「1」と「1」は同一じゃなくて、
なぜかナゾの比率が生まれるのかもしれません。
考えれば考えるほどアタマが混乱してきて、
自分でも何言ってるのかわかりませんが(笑)
最初に書いたように「たぶん間違ってる事」をヌケヌケと書きました。
魔方陣発掘する前から、10年20年前から思いついて、古いノートに
書き込んでた数列です。それを吐き出せてスッキリした気分です。
「こんなもの読ませんな!」ってご批判は甘んじて受けます・・・m(_ _)m